选手B根据选手A提供的关键几何板信息，完成阿基米德十四巧板拼图。两队同时开始挑战，其中任意一方完成阿基米德十四巧板拼图，另一方则停止作答，作答正确得1分，作答错误对方得1分，共三轮，率先赢得两分的队伍获胜。

　　数图在上周“数字迷阵”项目中已经亮过相，本周它被赋予了五颜六色，变得更加艳丽。如图所示，在6×6的方格中，需要根据数字及其色彩，在空白方格填上相应颜色，找出3块几何板的隐藏信息。然而选手现场要挑战的是12×12的方格，计算量更大，难度系数更高。

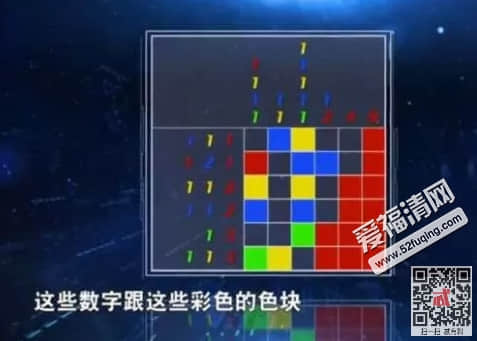
　　经过科学计算，十四巧板一共有17152种可能的拼法，即使知道3块板的信息，最终找到一种可能性的计算量也是非常庞大的。